|
|
|
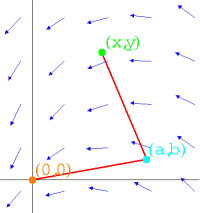
The planimter connects is fixed at (0,0) has an "elbow" at (a,b) and points to
(x,y). Both segments of length 1. Given (x,y), we can find (a,b) as a function of (x,y). The planimeter
vector field F(x,y) = (-(y-b(x,y),x-a(x,y)) has curl 1. The weel rotation of the
planimeter when (x(t),y(t)) traces a closed curve is the line integral of the
vector field F along the curve. The key observation is that the field F has curl(F)=1
as can be verified with a simple computation (see the four lines of Mathematica below).
By Greens theorem, the total wheel rotation is the area of the enclosed region R.
|
Links:
Mathematica Code:
(* Mathematica verfies that the planimeter vector field has curl(F) = 1 *)
(* Oliver Knill, Harvard University, 9/2000, final form 8/2005 *)
s=Simplify[Solve[{ (x-a)^2+(y-b)^2==1, a^2+b^2==1 }, {a,b}]];
aa[x_,y_]:=a /. s[[1,1]]; bb[x_,y_]:=b /. s[[1,2]];
F[x_,y_]:={-(y-bb[x,y]),x-aa[x,y]};
curlF=D[F[x,y][[2]],x] - D[F[x,y][[1]],y];
Simplify[curlF==1]
|