 Fall 2003 |
|
|
Fall 2003 |
|
|
In the movie "Good Will Hunting",
the main character Will Hunting (Matt Damon)
solves a blackboard problem, which had been assigned as a challenge to a
linear algebra class. [ Update: 2013: Non flash video Update: Jan 2017: A larger size clip with the math only.] Update: May 2017, Thanks to Mark W. Wiemer for some corrections to 3) and 4) which are here applied. |
|
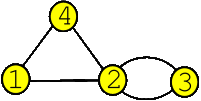
| The adjacency matrix L encodes the graph. The entry Lij is equal to k if there are k connections between node i and j. Otherwise, the entry is zero. Problem 2 asks to find the matrix which encodes all possible paths of length 3. |
Generating function. To a graph one can assign for
pair of nodes i,j a series
 ,
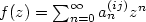where an(ij) is the number of walks from i to j with n steps.
Problem 3) asks for a formula for f(z) and in
problem 4) an explicit expression in the case i=1,j=3.
|
| Solution to 1). The adjacency matrix L is |
|
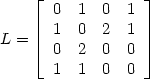
| Solution to 2). [L2]ij is by definition of the matrix product the sum Li 1 L1 j + Li 2 L2 j +... + Li n Ln j. Each term Li k Lk j is not 0 if and only if there is at least one path of length 2 going from i to j passing through k. Therefore [L2]ij is the number of paths of length 2 leading from node i to j. Similarly, [Ln]ij is the number of paths of length n going from i to j. The answer is |
![L^3 = [2 & 7 & 2 & 3 \\ 7 & 2 & 12 & 7 \\ 2 & 12 & 0 & 2 \\ 3 & 7 & 2 & 2]](img/07.gif)
|
Solution to 3). The
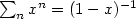for the summation of a geometric series holds also for matrices:
![f(z) = \sum_{n=0}^{\infty} [L^n]_{ij} z^n = [\sum_{n=0}^{\infty} L^n z^n)]_{ij} = [(1-Lz)^{-1}]_{ij}](img/03.gif) .
Cramer's rule for the inverse of a matrix
is A-1 = adj(A)/det(A)
where adj(A) is the adjugate matrix
of A, the transpose of the cofactor matrix of A.
Therefore, we have for every i and j the generating function adj(1-z L)ij/det(1-z L) which is a rational function.
| |
|
Solution to 4). Especially, when i=1 and j=3,
we get adj(1-zL)13 = 2 z2 + 2 z3 and
det(1-zL) = 1-7 z2 - 2 z3+4 z4.
The result can be written as
(2 z2+2z3)/(1-7 z2 - 2 z3+4 z4)
which simplifies to 2z^2/(1-z-6z^2+4z^3). Handout [PDF] | |
Here is Mathematica code to check this:
L={{0,1,0,1}, {1,0,2,1}, {0,2,0,0}, {1,1,0,0}}
K[z_]:=IdentityMatrix[4] -z*L;
Adj[A_,i_,j_]:=Module[{B=A},B=Delete[B,i];B=Transpose[B];B=Delete[B,j];B];
(-1)^(1+3) Det[Adj[K[z],1,3]]/Det[K[z]]
(* check with Inverse[K[z]][[1,3]] *)
|
|
|
