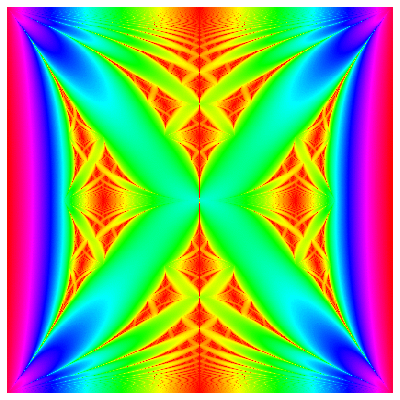
The picture below illustrates a function f(x,y) of two variables which is defined
using determinant of matrices.
For rational y=p/q form f(x,y) = log[ | det (L(y) -x) | ]/q, where L(y) is a
(q x q) matrix with side diagonal entries 1 and diagonal entries
V(k) = 2 cos(2 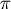 k p/q ): k p/q ):
| V(1) 1 0 ... 0 1 |
| 1 V(2) 1 ... ... 0 |
L(y)= | 0 1 ... ... ... ... |
| ... ... ... ... 1 0 |
| 0 ... ... 1 V(q-1) 1 |
| 1 0 ... 0 1 V(q) |
|
Physically, the x-coordinate is the energy. The y coordinate is related
to a magnetic flux.
The Hofstadter butterfly is the set, where f(x,y)=0. The picture to the right is colored
according to the value of f(x,y).
Mathematicians call the function f(x,y) a Lyapunov exponent. It is also defined for irrational
y through a limit.
See the Java applet.
|


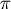 k p/q ):
k p/q ):