Number of Row Reduced 0-1 matrices
In one of the homework problems you looked for the number of 0-1 matrices which are row reduced. The general problem is very interesting. The answer is explicitly known for any nxn matrix.
The number of row reduced n x n matrices is given by the sequence
A006116, a sum of Gaussian Binomial coefficients.
It is the number of subspaces of a vector space over the field Z2
or the number of distinct binary linear codes of length n
or the number of Abelian groups in C2n.
The sequence starts as follows:
1, 2, 5, 16, 67, 374, 2825, 29212, 417199, 8283458, ...Here are all 15 nonzero 3x3 cases: 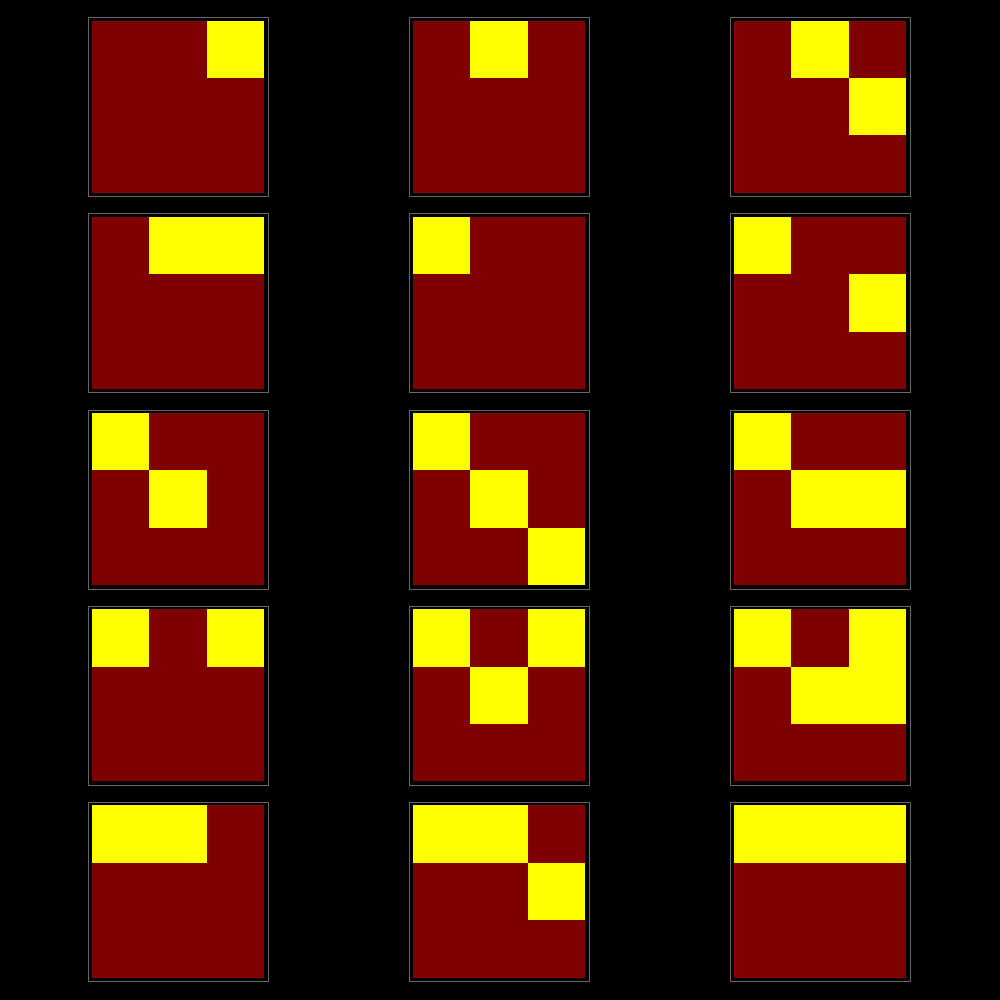
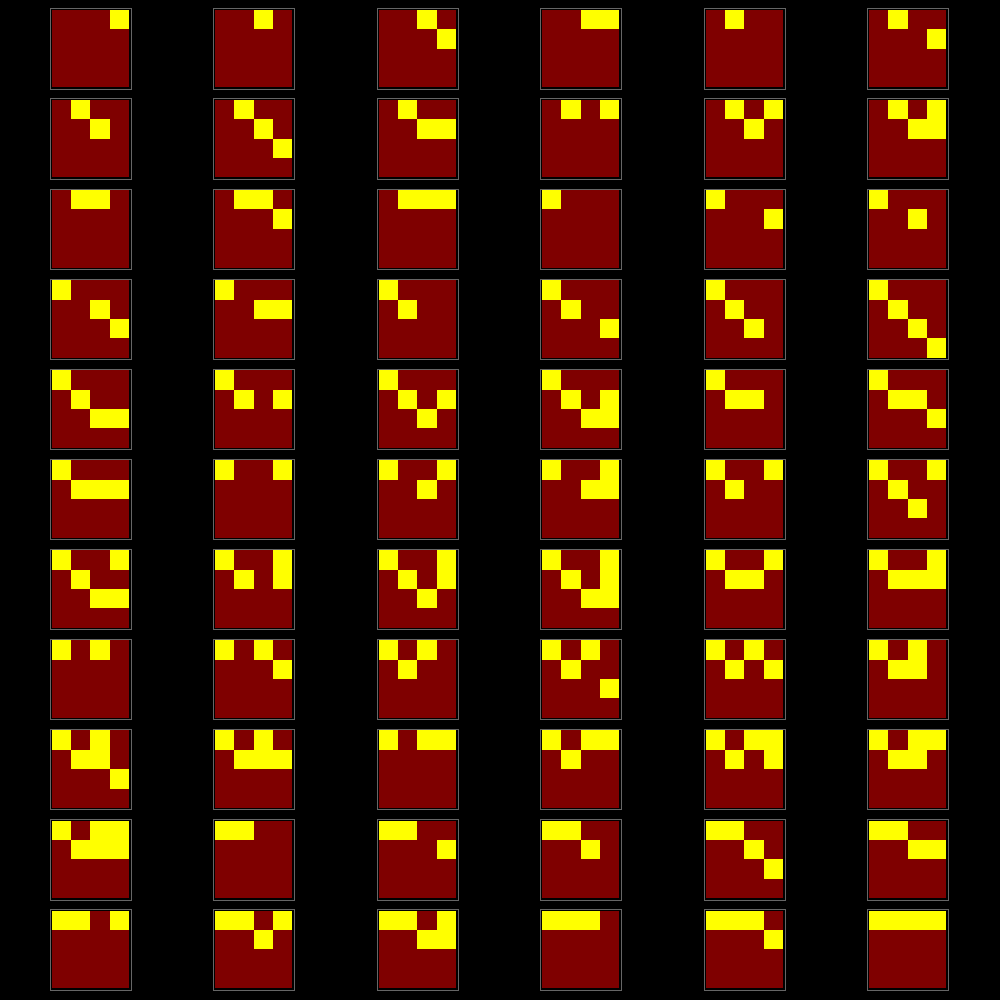

(* How many row reduced 0-1 matrices are there of size n x n ? *)
F[n_]:=Module[{i,u,m=n^2},
i[x_]:=Partition[PadLeft[IntegerDigits[x,2],m],n];
u=Map[i,Range[0,2^m-1]]; (* produces list of all 0-1 matrices *)
v=Union[Table[RowReduce[u[[k]]],{k,2^m-1}]];
w={}; Do[If[Sort[Union[Flatten[v[[k]]]]]=={0,1},
w=Append[w,v[[k]]]],{k,Length[v]}]; 1+Length[w]];
F[4]
When first computing this, I (Oliver) had not checked that the row reduced matrices
are still 0-1 matrices. Actually, they are not in general. Thanks to Jun Hou Fou
(whom you know from teaching 21a last semester) for pointing this out to me
and telling about the connection to the subspace problem and the sequence A006116.
Please send questions and comments to knill@math.harvard.edu
Math21b Harvard College Class Number:16325 Course ID:110989| Oliver Knill | Spring 2016 |
Department of Mathematics |
Faculty of Art and Sciences |
Harvard University,
[Canvas, for admin],
Twitter
|